１．X線イメージング（レントゲン）

Ｘ線は波長の短い電磁波（光）で、図1に示すように物質に対する透過能が高いことが大きな特徴の一つです。Ｘ線イメージング（レントゲン）は、この高い透過能を利用して物体の影絵を計測する方法です。

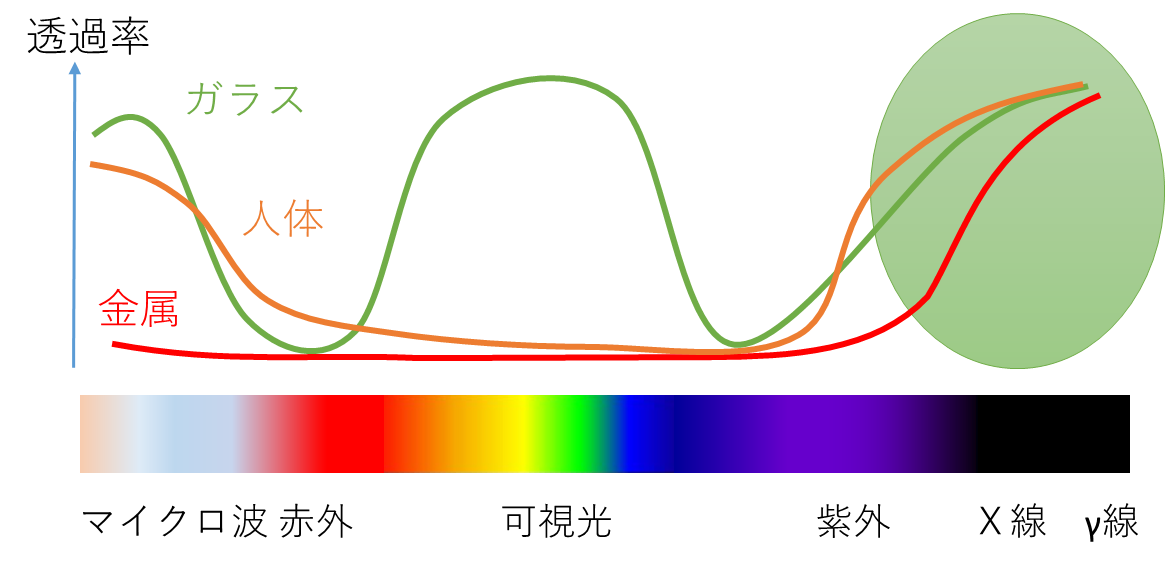図1　X線はどのような物質に対しても透過率が高い

被写体に照射するＸ線の強度をI₀としたとき、透過した強度Iは

　　I=I₀ exp(-ut）

となります。ここで、uは線吸収係数、tは被写体の厚さです。uは一般に重い（密度が大きい）ほど大きくなり、Ｘ線は透過しにくくなります。したがって、レントゲンは被写体内部の重い場所ほど暗く、軽い場所ほど明るく写ります。（但し、Ｘ線フィルムは明暗が反転して現像されるので、重いところほど明るく表示されます。）

２．X線CT

X線の吸収は、物体の厚さtと線吸収係数（～密度）uの２つの変数となっているため、図２のように厚さと線吸収係数が異なっていても積が同じ物体を区別することはできません。

図２　レントゲンではutが同じだと区別できない

また、吸収はX線が透過する透過する方向について積算した値となるために、物体の前後関係を検出できない（深さ分解能がない）という問題があります（図３）。

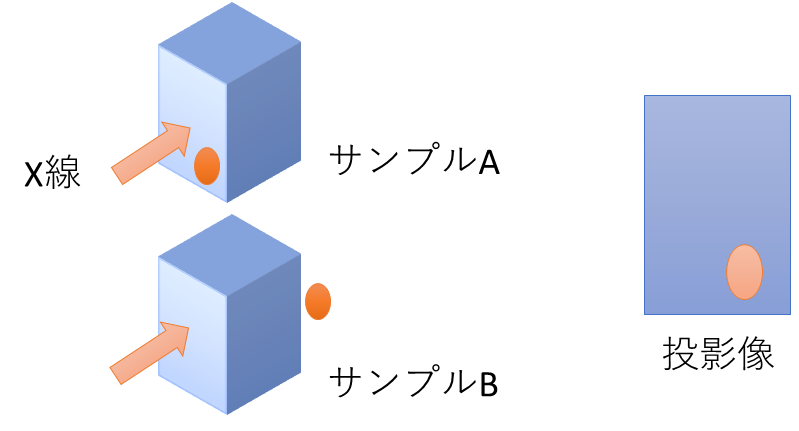図３　奥行き方向も区別できない

この問題を解決する方法として、X線CTが発明されました。以下、非常に単純化したモデルでその原理を説明します。

図４のように３ｘ３のセルで構成されたサンプルを考えます。各セルの線吸収係数をu_i,jとし、厚さはtで同じとします。CTとは、この線吸収係数の分布を求めることです。

強度I₀のX線を左から入射したとき、セル11を透過したX線の強度は

　I₁₁=I₀exp(-u₁₁t)

となります。ここで、u₁₁はセル11の線吸収係数です。次のセル12の場合は、I₁₁が入射X線強度になるので、

　I₁₂=I₁₁exp(-u₁₂t)

となり、最後のセルから出射するX線の強度I₁₃は同様に

　I₁₃=I₁₂exp(-u₁₃t)

となります。上式について、I₀を用いると、

　I₁₃=I₀exp(-u₁₁t)exp(-u₁₂t)exp(-u₁₃t)

　　=I₀exp(-(u₁₁+u₁₂+u₁₃)t)

とまとめることができます。同様に、セル23及び33から出射するX線は

　I₂₃=I₀exp(-(u₂₁+u₂₂+u₂₃)t)

　I₃₃=I₀exp(-(u₃₁+u₃₂+u₃₃)t)

となります。以上から、expはかかっていますが、各セルの線吸収係数の加算だけを考えれば良いことが判ります。

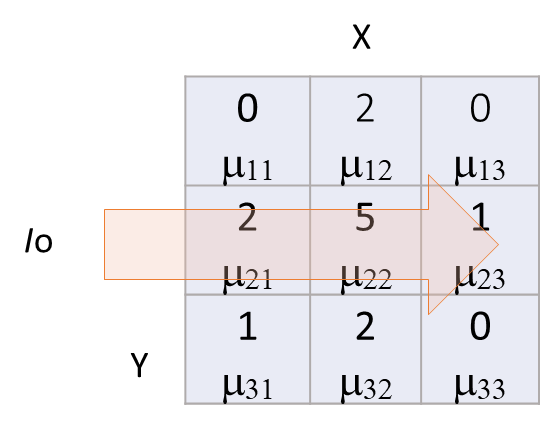図４　X線CTの原理１

左、上、右、下の方向からX線を照射した場合、線吸収係数の和は図５のようになります。

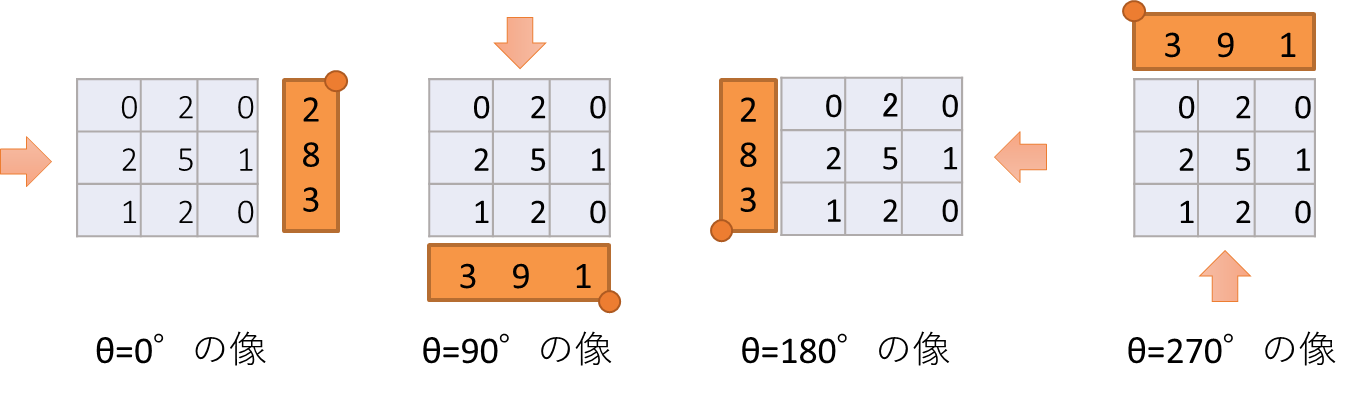図５　各方向について線吸収係数の和を計算

縦軸を角度、横軸を各和として並べ直すと図６のようになります。この図のことをSinogram（サイノグラム、或いはシノグラム）と呼びます。このデータは計測で得られますので、このサイノグラムから線吸収係数の分布を計算で求めることになります。

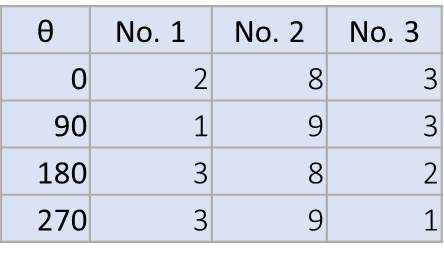図６　図５をまとめた表：サイノグラム

具体的には、図５の逆の手順で計算を行います（図７）。

1. 全てのセルを０にする
2. 左からX線を照射して得たデータは、右から各セルに値を加算する。
3. 同様にX線を上から照射して得たデータは、下から各セルに値を加算する。
4. 右、及び下から照射して得たデータも同様に加算する
5. 角度データ数（この場合は４）で全てのセルの値を除算する

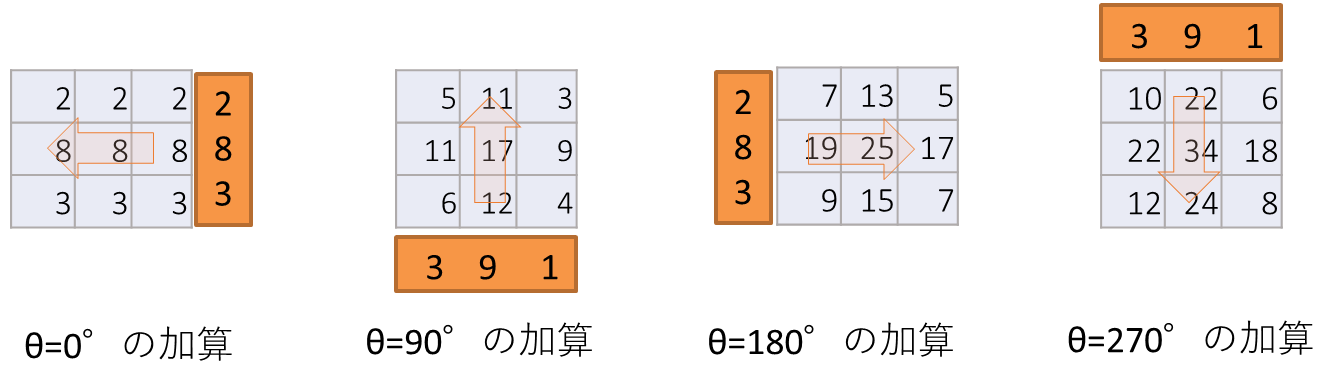図７　CT（逆投影）の計算

このように、逆に投影してデータを加算していくので、「逆投影（back-projection）」と呼びます。この逆投影計算の結果と、元の線吸収係数の分布を比較すると、ある程度傾向は似ていることが判ります。（図８）

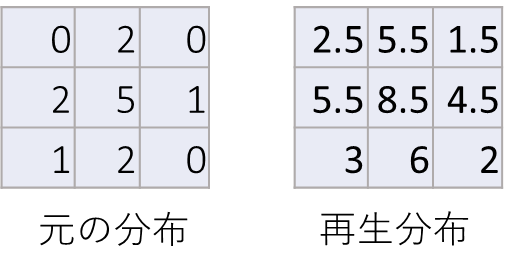図８　元の分布と逆投影計算（再生）による結果との比較

両者が完全に一致していないのは、中心領域の加算が多くなるなどが主な原因になります。この問題を解決するために、一般には高周波強調フィルターをかけた（コンボリューション）後に逆投影計算を行います。このため、Filtered back-projectionと呼ばれています。フィルターにはいろいろな種類がありますが、最も有名なフィルターはShepp-Loganと呼ばれるフィルターです。

実際のCT計測は

1. サンプルを回転して、投影像を複数枚取得
2. 各位置でサイノグラムを計算
3. フィルターをコンボリューション
4. 逆投影

として行います。

図１０はフィルター無し、SLフィルター、ノイズ低減フィルター（フィルターの高周波成分を抑制）で再構成した断面像です。

　図１０　各フィルター関数による再構成例（電解コンデンサー）